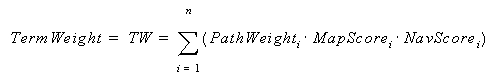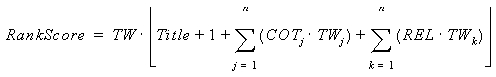The ranked lists of MeSH headings produced by all of the methods described so far must be clustered into a single, final list of recommended indexing terms. The task here is to provide a weighting of the confidence or strength of belief in the assignment, and rank the suggested headings appropriately. There are a number of factors that can be recognized as playing a role in that confidence. The method of finding the heading (the path), how much confidence is available in how the method found the heading (the goodness of the match), the location in the text of the nominal phrase that led to that suggestion (the location), and the semantic consistency of the suggested heading with the other suggested headings (the corroborating evidence).
The clustering algorithm uses two formulas for finding the rank score. One is for the weight of a given MeSH heading (or term), the second for the rank order. The term weight formula is:
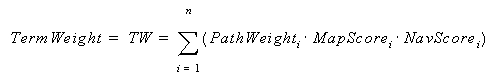
where i represents a single occurrence of the suggestion of one MeSH heading.
Assigning a weight to the overall method of finding the heading (the Path Weight) allows one to discount a method appropriate to strengths. For example, a certain path might not be very specific, but have some sensitivity in suggesting headings which would otherwise not occur. When headings found by other paths offer corroborative evidence for a heading suggested by this method, the additional confidence gained might be helpful.
The goodness of the match, i.e., how much confidence to place in a given heading, depends on the method used to find the heading. The possibilities are:
- A phrase identified in text is an exact match to a MeSH term. Equivalently, it might have been a match to a UMLS term which was a synonym of a MeSH term.
- Of lesser significance is an exact match to a UMLS term which is then be mapped to a MeSH heading using the Restrict to MeSH method.
- Another possibility is that the phrase is an inexact, or approximate, match to a UMLS term, which is either a synonym of a MeSH heading or mapped to MeSH.
Thus, each time a MeSH heading is suggested, a weighting can be given to that suggestion. This is accomplished using both a
MapScore and a
NavScore. The MapScore reflects the confidence in the mapping to a UMLS term, the NavScore the confidence in navigating from a UMLS term to a MeSH Heading.
A ranking score for each suggested MeSH heading can be calculated by the following formula:
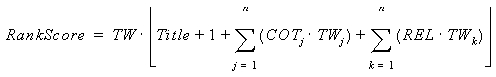
where j and k represent other suggested MeSH headings, semantically related to the suggested heading by either co-occurrences in MEDLINE or by occurrence in the same hierarchy in MeSH.
With regard to the importance of location, the main consideration was whether or not the phrase leading to a heading suggestion was mentioned in the title. All other things being equal, indexers know that things mentioned in the title of the article are probably more important than other concepts mentioned in the article. Similarly, if the heading was suggested by a phrase occurring in the title, it should be given more weight. The additional weight is added as a constant in the formula.
Semantic consistency can be thought of as corroborative evidence for the goodness of a suggestion. It is identified by relationships that a suggested heading has with other suggested headings. These relationships might be either the occurrence in the same hierarchy (as parents or siblings), or as known co-occurring headings in MEDLINE. This latter evidence needs to be weighted according to a normalized frequency of this co-occurrence. The normalized frequency times a constant becomes the COT weight. The former evidence is the REL weight, and is a simple constant.
The overall Rank Score can be altered by changing any of the constants (COT, REL, Title, PathWeight) or by changing the method by which the weight is calculated (NavScore and MapScore). Altering these values allows a number of experiments to be performed to evaluate the robustness of the weighting scheme, and to establish reasonable values for the constants.